多目的最適化
前章では、金属板の「最大変形量」という一つの目的関数のみを対象にその値を最小化するという問題を扱ってきました。
しかしながら、現実の最適化問題では、一つの目的関数だけでなく、複数の目的関数を同時に最小化したいという場合が多くあります。
このように、複数の目的関数を同時に最適化することを「多目的最適化」と呼びます。なお、これまでどおりの一つの最適化問題のみを扱う最適化は、「単目的最適化」あるいは「単一目的最適化」と呼ばれます。
目的関数が\(m\)個である多目的最適化の場合、最適化システムは次の図のように表すことができます。
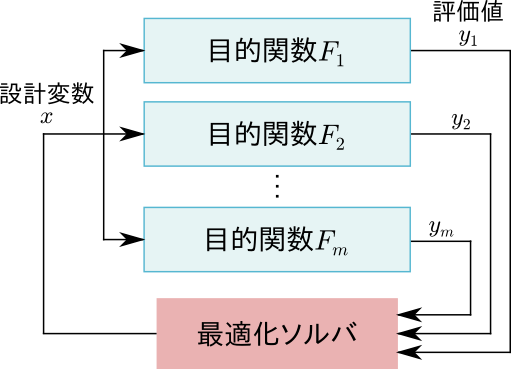
あるいは、前章でも示した次の図において、評価値がベクトル\(\mathbf{y}=(y_1,\ldots,y_m)\)であるものとして考えることもできます。
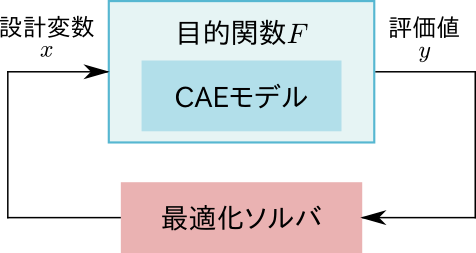
いずれにしても評価値は複数の実数の組となり、最適化ソルバも複数の評価値を同時に扱うことが可能な多目的最適化専用のソルバを使用する必要があります。
以下で、金属板の搬送パターン最適化問題に対し、実際に多目的最適化を適用していきましょう。
変数変換器
前章の単目的最適化における変数変換器では、無次元化した搬送パターン\(S(T)\)を要素数2の実数値ベクトル\(\mathbf{x}=(x_1,x_2)\)によって表現しました。これはすなわち、2自由度で表現した、といえます。
本章では、2個の目的関数を最小化する多目的最適化を行うため、最適化問題の難易度や複雑さが増加しているといえます。
したがって、搬送パターンの定義の自由度も増加させなければ、十分な最適解が得られない可能性があります。
そこでここでは、搬送パターン\(S(T)\)を4自由度、すなわち要素数4の実数値ベクトル\(\mathbf{x}=(x_1,x_2,x_3,x_4)\)で表現することとし、このとき数式としては、次のような7次多項式として定義することとします。
\begin{align*}
S(T) = T^7 + 7T^6(1-T) + 21x_1T^5(1-T)^2 + 35x_2T^4(1-T)^3\\
{}+ 35x_3T^3(1-T)^4 + 21x_4T^2(1-T)^5
\tag{1}
\label{eq:7th_polynomial}
\end{align*}
また、設計変数\(\mathbf{x}\)の範囲は次のとおりとします。
\begin{align*}
\mathbf{x} \in [0,1]^4
\end{align*}
このように、設計変数の自由度を増加させることで、より多様な搬送パターンをカバーすることができ、より優れた解を導出できる可能性が高くなります。
ただし、設計変数の自由度の増加に伴い、「解空間」の次元も増加するため、最適化においてより多くの繰り返し計算(目的関数の計算)が必要となります。
評価値計算器
評価値計算器も、目的関数が2個であることから、次の2式で定義します。
\begin{align*}
y_1 = \max_t |\varepsilon (t)|
\tag{2}
\label{eq:evaluator1}\\
y_2 = \max_{t_\mathrm{c} \le t} |\varepsilon (t)|
\tag{3}
\label{eq:evaluator2}
\end{align*}
式(\(\ref{eq:evaluator1}\))は、前章における評価値計算器とまったく同じであり、全時間区間における金属板の変形\(\varepsilon(t)\)の最大量を表しています。
また式(\(\ref{eq:evaluator2}\))は、搬送終了時刻\(t_\mathrm{c}\)以降における変形\(\varepsilon(t)\)の最大量を表しており、これにより残留振動の大きさを評価することができます。なお本コラムでは、\(t_\mathrm{c}\)は0.1 sとなっています。
これらの二つの評価値\(y_1\)および\(y_2\)を\(\varepsilon(t)\)のグラフ上で図示すると次のようになります。
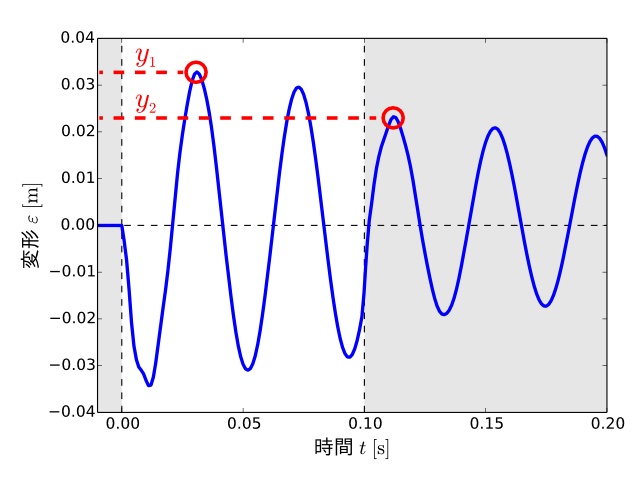
\(y_1\)と\(y_2\)の関係は、常に\(y_1 \ge y_2\)であり、金属板の最大の変形が残留振動において生じた場合に\(y_1 = y_2\)となります。
最適化問題の定式化と最適化ソルバ
上記で定義した設計変数\(\mathbf{x}\)から評価値\(y_1\)および\(y_2\)までの目的関数をそれぞれ\(F_1\)および\(F_2\)とすると、本最適化問題は次式で定義できます。
\begin{align*}
\mathrm{minimize}\quad& y_1 = F_1(\mathbf{x}) \quad \mathrm{and} \quad y_2 = F_2(\mathbf{x})\\
\mathrm{subject\ to}\quad& \mathbf{x} \in [0,1]^4
\end{align*}
本章では、この最適化問題を「NSGA-II」と呼ばれる最適化ソルバによって解くことにします。
NSGA-IIは、「遺伝的アルゴリズム」と呼ばれる最適化手法の一種で、多目的最適化に対応したソルバーです。
遺伝的アルゴリズムは、生物が世代交代するなかで進化していく過程を模擬した最適化のアルゴリズムです。汎用性が高く、扱いやすい手法としてCAEを利用した最適化でもたびたび用いられます。
遺伝的アルゴリズムでは、設計変数\(\mathbf{x}\)の具体的な値一つを「個体」として表現します。つまり本コラムの場合は、一つの搬送パターンが一つの個体となります。
さらに個体は、一定個数の集合である個体集団を形成し、その集団は、「世代」ごとに新たに個体を生成し、劣った個体と入れ替えながら進化を進めていくことで最適化が行われます。
なお、ここでは、この世代あたりの個体数を100、最適化完了までの世代数を50として設定することにします。
最適化結果
以上で定義した多目的最適化システムによって、金属板の変形および残留振動を最小化する搬送パターンの最適化をおこないました。
この最適化によって生成したすべての搬送パターン、すなわち全個体の評価値に対する分布図を次に示します。
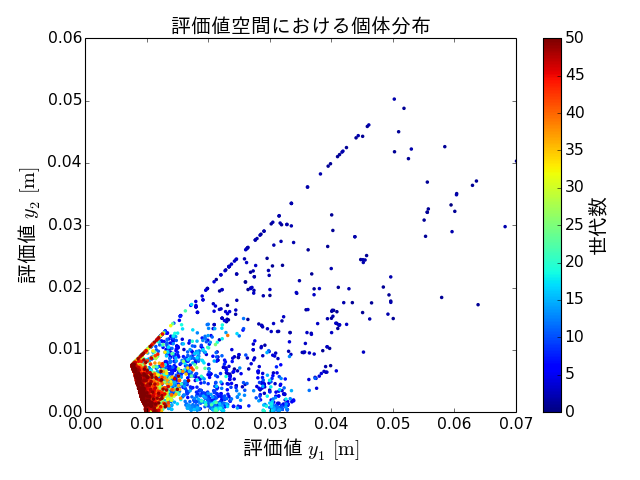
図中の1点が一つの個体を表しており、さらに点の色は、その個体が生成された世代を示しています。
本最適化問題における理想上の最適解は、\((y_1,y_2)=(0,0)\)に位置する個体であり、この図でも、世代が進むに連れてその理想的な最適解のある方向へと個体の探索が進んでいることがわかります。
しかしながら、この理想的な最適解は現実的には存在しないため、それにより近い個体を実用上の最適解とする必要があります。
この最適解の候補が密集している付近の拡大図を次に示します。
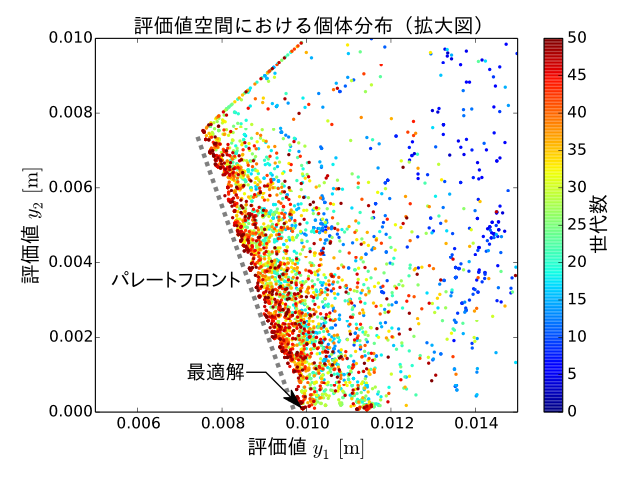
多目的最適化における最適解は、一般的に、「パレート最適」と呼ばれる概念にもとづいて決定されます。
ある個体集団におけるある個体がパレート最適である場合、その個体の各評価値について、それらすべての値を改善する(または同等である)評価値を持つような個体は、その個体集団内には存在しません。
そのような「パレート最適解」は、通常、複数あるいは無限に存在し、それらのパレート最適解の集合が形成する形状を「パレートフロント」と呼びます。
本最適化の場合、パレートフロントは、図中の点線のような直線的な形状となっています。
多目的最適化では、このパレートフロント上のパレート最適解の中から、評価値以外の要素なども考慮することで、唯一の最適解を決定することになります。
ここでは、残留振動を表す評価値\(y_2\)の値を最優先することとし、それが最小となる、図中の矢印で示した個体を最終的な最適解とすることにします。
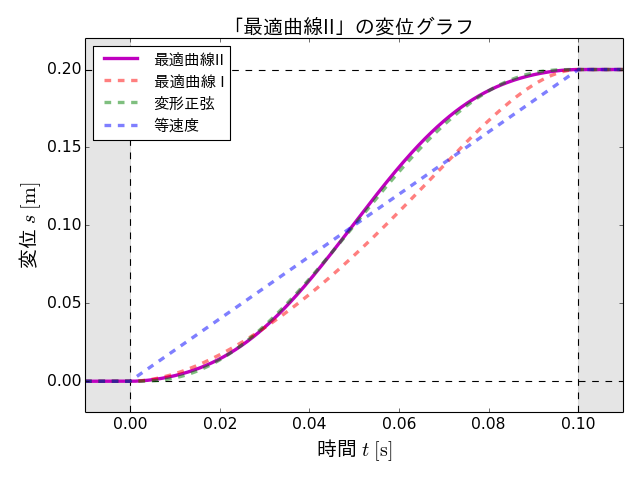
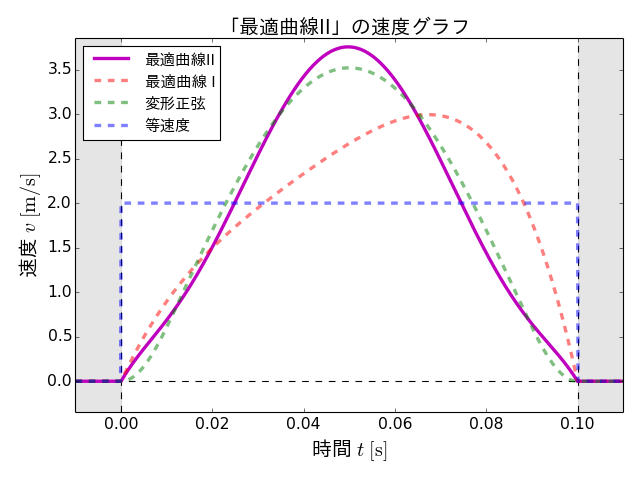
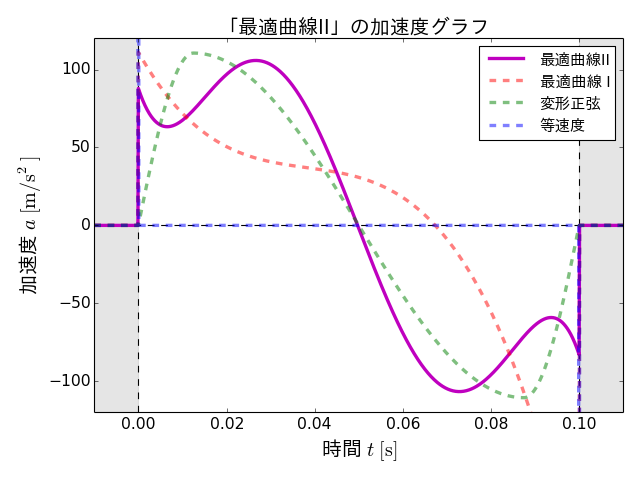
この最適搬送パターンの変位、速度、加速度の各グラフ、さらに各設計変数の値および評価値を以下に示します。また、この搬送パターンを「最適曲線II」と呼ぶことにします。
| \(x_1\) | 0.901 |
|---|---|
| \(x_2\) | 0.907 |
| \(x_3\) | 0.109 |
| \(x_4\) | 0.105 |
| \(y_1\) | 0.00990 |
| \(y_2\) | 0.000100 |
最適曲線IIは、変位グラフでは、変形正弦にかなり近い形状となっています。また、加速度の最大は、最適曲線Iよりも小さく、変形正弦とほぼ同等であることがわかります。
次に、最適曲線IIによる搬送シミュレーションの結果のアニメーションと、そのときの金属板の変形のグラフを示します。
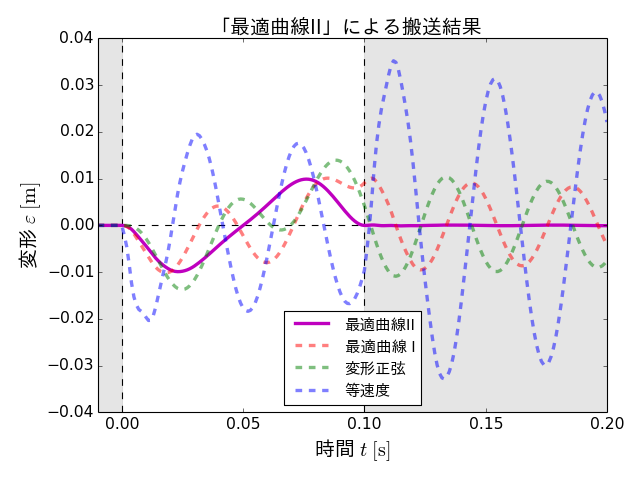
これらのアニメーションとグラフより、最適曲線IIによる搬送によって、金属板はちょうど1往復分の変形動作がおこなわれ、その後、搬送が完了すると同時にもとの直線的な形状へと戻り、残留振動はほぼゼロに抑えられていることがわかります。
したがって、この多目的最適化により、残留振動がなく、変形を最小とすることを可能とする、ほぼ完璧な搬送パターンを導出することができました。
最適化の結果、残留振動がほぼゼロで、搬送時の変形も最小化される良好な搬送パターンを求めることができました。本コラムでは、最適化の対象として搬送パターンという物体の動作の関数を扱い、またCAEとしては変形解析を扱ってきました。
しかし実際の問題では、物体の動作だけでなく、さまざまな設定パラメータや形状なども最適化の対象となり、またCAEとしては変形解析以外にも、熱流体解析や応力解析など、扱う現象も異なります。
それでも基本的には、最適化システムの「変数変換器」と「評価値計算器」を適切に定義し、そして適切な「最適化ソルバ」を用いることで、ほとんどの問題を最適化することができます。
ぜひ皆さまの業務でも最適化を導入し、最適な製品や手法の開発を実現していきましょう。

