最適化システム
CAEを利用して最適化をおこなうためには、CAEモデルに加えて他にいくつかの要素が必要となります。これらの要素を組み合わせた最適化のための全体のシステムを「最適化システム」と呼ぶことにしましょう。
一般に、最適化システムは次のような図として表すことができます。
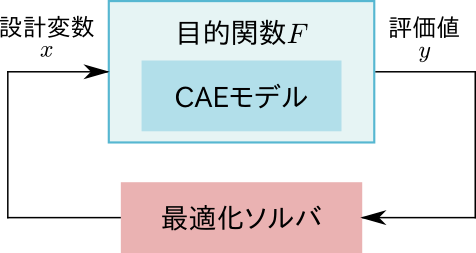
最適化システムは、基本的には「目的関数」と「最適化ソルバ」から構成されます。
目的関数は、「設計変数」に応じて「評価値」が出力される関数のことで、最適化したい問題そのものを表しています。したがってここでは、CAEモデルもこの目的関数の一部となります。
一方で最適化ソルバは、目的関数に対し、評価値が最良となるような設計変数を求める計算器のことです。最適化アルゴリズムや最適化手法などとも呼ばれます。
最適化ソルバにはさまざまな種類があり、それぞれ扱うことのできる設計変数および評価値の「型」が決まっています。
ここで型とは、数値であれば整数値や実数値、あるいはスカラーやベクトルといった種類のことを意味しています。
(※設計変数の場合は、数値のほかにも、関数や順列・組合せなどの型もありえます。)
多くのソルバでは、設計変数の型として実数値ベクトル(すなわち複数個の実数値の組)を、評価値の型として実数値スカラー(すなわち1個の実数値)を対象とします。したがって本コラムにおける最適化システムでも、これらの型を対象としていきます。
このとき数学的には、設計変数は\(\mathbf{x}=(x_1,\ldots,x_n)\)(ただし\(n\)は要素数)として、また評価値は単に\(y\)としてそれぞれ表すことができます。
結局、最適化は次のような流れによっておこなわれます。
- 最適化ソルバが、初期値として適当な設計変数を目的関数に入力する。
- 目的関数が、入力された設計変数をもとに評価値を計算し、出力する。
- 最適化ソルバが、その評価値をもとに、より優れた評価値を持つ可能性のある設計変数を推測し、それを目的関数に入力する。
- 以後、終了条件が満たされるまで2.と3.を繰り返す。
さて、ここまでで最適化システムの概要はわかりましたが、実際に最適化システムを構築するためにはどのようにしたら良いのでしょうか?
最適化ソルバはあとから適当なものを選べば良いとして、問題は前章で構築したCAEモデルをいかにして目的関数に組み込むかです。
ここで一度、このCAEモデルがどのようなものであったか整理してみましょう。
このCAEモデルは、搬送パターンの変位\(s(t)\)を入力することで、金属板の変形\(\varepsilon (t)\)が出力されるものでした。
つまり、これを図で表すと次のようになります。

ここで、この図と上で示した最適化システムの図を比較することで、目的関数のなかに追加すべき要素が見えてきます。
すなわち、まずは設計変数\(\mathbf{x}\)から搬送パターン\(s(t)\)へ変換する要素が必要となります。この要素を「変数変換器」と呼ぶことにしましょう。
さらに、金属板の変形\(\varepsilon (t)\)を評価値\(y\)に変換する要素も必要です。これを「評価値計算器」としましょう。
これらの二つの要素を加えることで、最適化システムは最終的に次のように表すことができます。
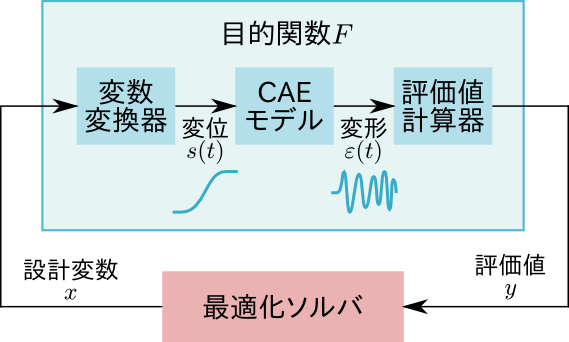
以下では、これらの変数変換器および評価値計算器を定義することで、まずは目的関数を完成させましょう。
変数変換器
変数変換器は、設計変数である実数値ベクトル\(\mathbf{x}\)から、搬送パターンを表す関数\(s(t)\)へと変換する要素でした。
このような変換を実現するには、さまざまな方法が考えられますが、ここでは比較的単純な多項式を用いた方法を採用してみます。
また、実数値ベクトル\(\mathbf{x}\)の要素数\(n\)も任意の値とすることができますが、これも簡単な\(n=2\)として設定することとします。このとき設計変数は\(\mathbf{x}=(x_1,x_2)\)となります。
具体的な方法を示す前に、簡単化のためにまず、関数\(s(t)\)を無次元化した関数\(S(T)\)を考えます。
ここで、\(S\)は無次元変位、\(T\)は無次元時間であり、それぞれ搬送開始時の値が0、搬送終了時の値が1となります。
つまりこの\(S(T)\)は次のようなグラフとして表すことができます。
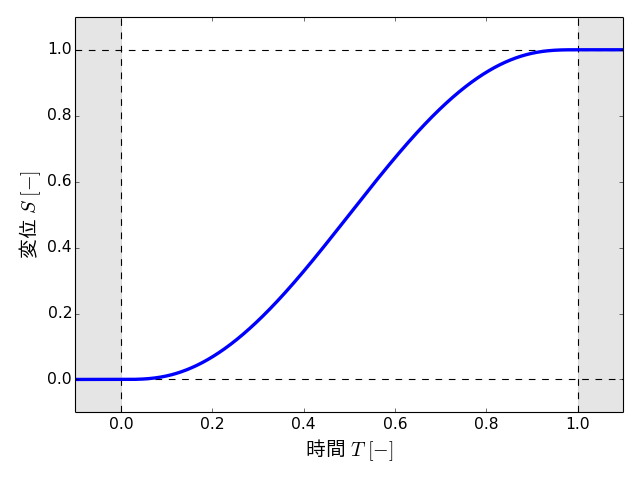
この無次元化した関数\(S(T)\)を設計変数\(\mathbf{x}=(x_1,x_2)\)を用いて次のような5次多項式として表現することとします。
\begin{align*}
S(T) = T^5 + 5T^4(1-T) + 10x_1T^3(1-T)^2 + 10x_2T^2(1-T)^3
\tag{1}
\label{eq:5th_polynomial}
\end{align*}
また、設計変数\(\mathbf{x}\)の範囲は次のとおりとします。
\begin{align*}
0 \le x_1 \le 1,\quad 0 \le x_2 \le 1
\end{align*}
これをまとめて書けば、次のようになります。
\begin{align*}
\mathbf{x} \in [0,1]^2
\end{align*}
式(\(\ref{eq:5th_polynomial}\))で定義した\(S(T)\)は、設計変数\(x_1\)および\(x_2\)に値を設定することで、その関数としての形が定まります。
実際に、\(x_1\)および\(x_2\)にいくつか代表的な値を設定し、そのときの\(S(T)\)をグラフ化した結果が次の図です。
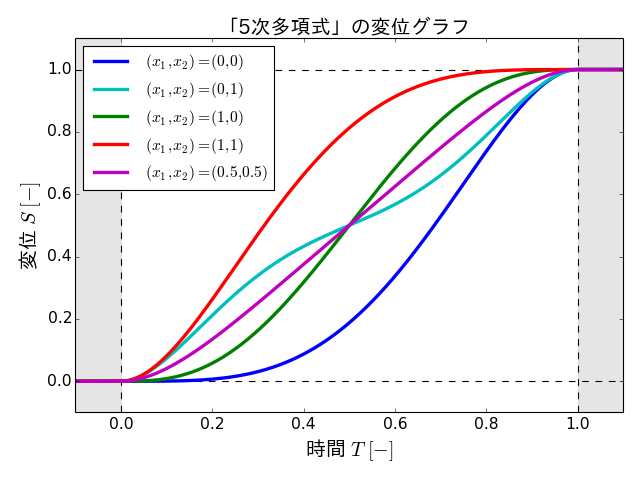
\(x_1\)および\(x_2\)の値が変わることで、\(S(T)\)もさまざまな形を取ることがわかります。
また、この\(S(T)\)のもう一つの特徴として、\(x_1\)、\(x_2\)の値に関わらず、搬送開始時(\(T=0\))および搬送終了時(\(T=1\))における接線の傾きが常に0となります。
これにより、式(\(\ref{eq:5th_polynomial}\))によって表される\(S(T)\)は、第1章で取りあげた変形正弦の場合と同様に、速度の急激な変化がなくなることで、金属板の変形を抑制する効果を持ちます。
次に、この無次元化した関数\(S(T)\)を本来の関数\(s(t)\)に変換する必要があります。搬送時間が\(t_\mathrm{c}\)、搬送距離が\(s_\mathrm{c}\)であるとき、次式によって変換することができます。
\begin{align*}
s(t) = s_\mathrm{c} \cdot S(t/t_\mathrm{c})
\tag{2}
\label{eq:Stos}
\end{align*}
なお本コラムでは、搬送時間\(t_\mathrm{c}\)を0.1 s、搬送距離\(s_\mathrm{c}\)を0.2 mと定義しています。
結局、式(\(\ref{eq:5th_polynomial}\))および(\(\ref{eq:Stos}\))を用いることで、設計変数\(\mathbf{x}\)から搬送パターン\(s(t)\)へと変換することができ、両式を合わせて変数変換器となります。
評価値計算器
評価値計算器は、CAEモデルのシミュレーションから算出される金属板の変形\(\varepsilon (t)\)をもとに、最適化で用いる評価値\(y\)を計算する要素です。
一般的に、最適化ソルバは、関数である\(\varepsilon (t)\)を直接、評価指標として扱うことはできないため、この\(\varepsilon (t)\)を1個(ないしは数個)の実数である評価値に変換する必要があります。
ここでは、金属板の変形を最小化することを目的とし、評価値\(y\)を、変形\(\varepsilon (t)\)の絶対値の最大値として次式のように定義しましょう。
\begin{align*}
y = \max_t |\varepsilon (t)|
\tag{3}
\label{eq:evaluator}
\end{align*}
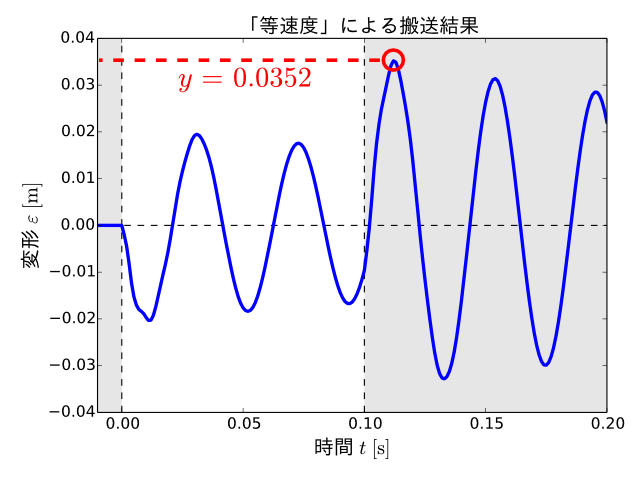
これは例えば、第1章で示した等速度での搬送結果でいえば、次の図の赤丸で示した部分が\(\varepsilon (t)\)の絶対値が最大となる点であり、その値は0.0352となります。
最適化問題の定式化
ここまでで、最適化システムのうち、目的関数の部分を完全に定義することができました。
ここで、この目的関数を\(F\)で表し、これを最小化する「最適化問題」として、次式のように定式化をおこないましょう。
\begin{align*}
\mathrm{minimize}\quad& y = F(\mathbf{x})\\
\mathrm{subject\ to}\quad& \mathbf{x} \in [0,1]^2
\end{align*}
一つ目の式の「\(\mathrm{minimize}\)」は、目的関数\(F(\mathbf{x})\)を最小化せよ、という意味になります。実際にはさらに、目的関数\(F(\mathbf{x})\)が最小となるときの設計変数\(\mathbf{x}\)を求めることを意味しています。
二つ目の式の「\(\mathrm{subject\ to}\)」は、制約条件を表しており、設計変数の定義域などを記述します。
ここでいま一度、目的関数の計算手順、すなわち設計変数\(\mathbf{x}\)から評価値\(y\)を算出する手順を確認しておきましょう。
まず、変数変換器である式(\(\ref{eq:5th_polynomial}\))および(\(\ref{eq:Stos})\)に設計変数\(\mathbf{x}\)を代入することで、搬送パターン\(s(t)\)が得られます。
次に、この搬送パターン\(s(t)\)をCAEモデルによる搬送シミュレータへ適用することで、金属板の変形\(\varepsilon (t)\)が得られます。
最後に、評価値計算器である式(\(\ref{eq:evaluator}\))に変形\(\varepsilon (t)\)を入れることで、評価値\(y\)を求めることができます。
最適化ソルバ
最適化システムを構成する最後の要素が、最適化ソルバです。
最適化ソルバを利用することで、上記で定義した最適化問題を自動的に解くことができます。
前述のとおり、最適化ソルバにはさまざまなものがあり、対象の最適化問題に合わせて適当なものを選択します。
なお、最適化ソルバの実態は、最適化問題の解法アルゴリズムが記述されたプログラムとなります。
ここでは、最適化ソルバとして「NEWSUMT」と呼ばれるソルバを用いることにしましょう。
NEWSUMTは、ニュートン法と呼ばれる手法に基づいた最適化ソルバであり、目的関数の勾配を利用して最適化をおこないます。
NEWSUMTを使用するにあたって、設計変数\(\mathbf{x}\)の初期値を一つ設定する必要があります。
ここでは、\(\mathbf{x}\)の定義域に対してちょうど真ん中の値である\(\mathbf{x}=(0.5,0.5)\)を初期値とします。
最適化結果
以上で定義した最適化システムを用いて、金属板の変形を最小化する搬送パターンの導出をおこないました。
得られた搬送パターンの変位、速度、加速度の各グラフを以下に示します。なお、この搬送パターンを「最適曲線 I」と呼ぶことにします。
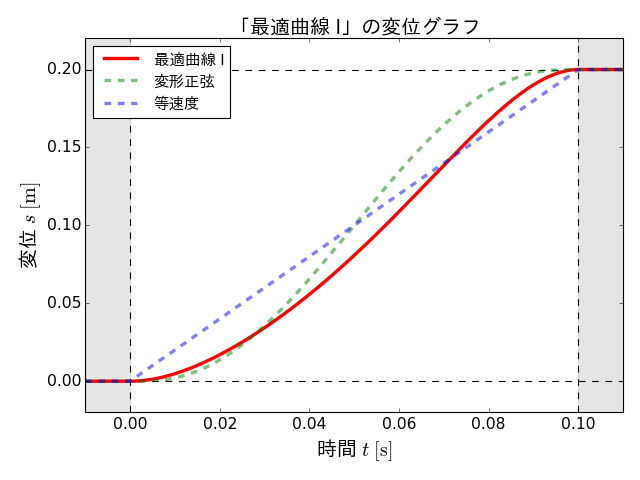
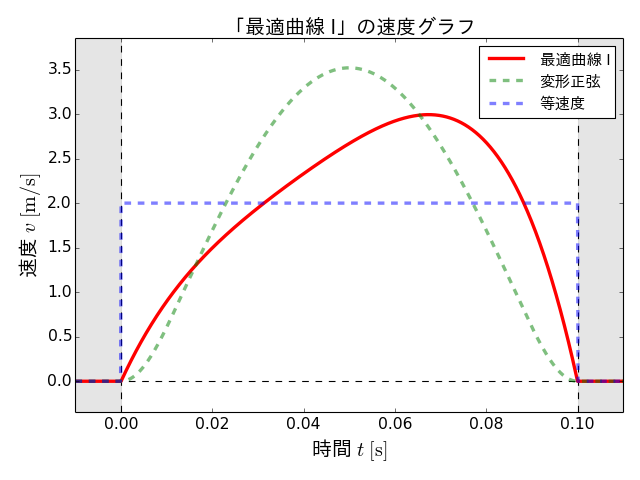
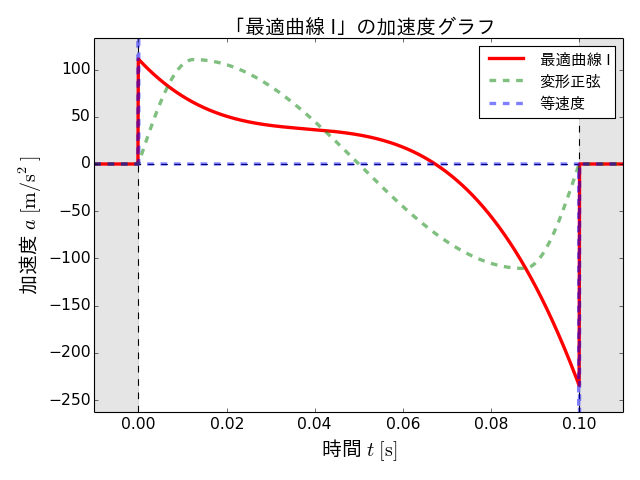
最適曲線 Iは変形正弦と比較して、速度の最大値が小さくなっている一方で、加速度の絶対値の最大値はかなり大きくなっています。
次に、最適曲線 Iによる搬送シミュレーションの結果のアニメーションと、そのときの金属板の変形のグラフを示します。
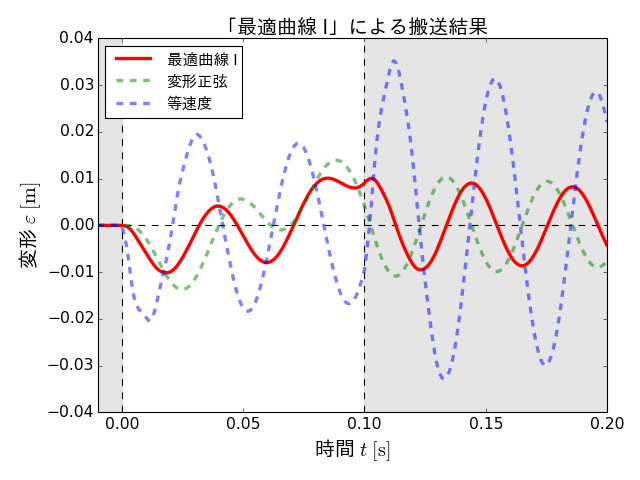
変形が最大となったのは、時刻0.018 sのときで、変形量は0.0101 mでした。
これらの結果より最適曲線 Iによる搬送は、比較的良好な搬送がおこなえていた変形正弦と比較しても、金属板の変形をさらに低減させることができたことがわかります。
ただし、搬送完了後にも金属板が振動し続けていることが少々気になる点ではあります。
最後に、最適曲線 Iの設計変数\(\mathbf{x}\)および評価値\(y\)を表としてまとめておきます。
| \(x_1\) | 0.414 |
|---|---|
| \(x_2\) | 0.278 |
| \(y\) | 0.101 |
本章では、搬送される金属板の変形を最小化するために、まず最適化システムの構築をおこない、さらに最適化ソルバとしてニュートン法の一種である「NEWSUMT」を用いることで搬送パターンの最適化をおこないました。
最適化の結果、前章で良好な搬送パターンであった変形正弦よりも、さらに優れた搬送パターンを求めることができました。
しかしながら、この最適な搬送パターンは確かに金属板の最大変形量は十分に小さくするものでしたが、搬送完了後にも振動的な変形が残ってしまっており、この点が実用上少々気になる点です。
このような金属板の残留振動も最小化する搬送パターンがあれば、これが本当に「最適な」搬送パターンであるといえるのではないでしょうか。
したがって次章では、多目的最適化をいることで、金属板の「最大変形量」と「搬送後の残留振動」をともに最小化する搬送パターンを導出してみましょう。

