問題の定義
本コラムでは、直線搬送機による物体の搬送プロセスを扱っていきます。
搬送物は、次のような薄板状の物体とします。
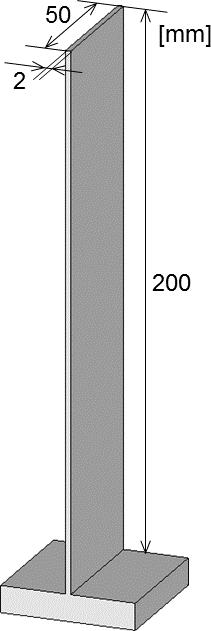
この物体は、板バネのような弾性体であり、次のような材料特性をもっているものとします。
| ヤング率 | 3.5×109 Pa |
|---|---|
| ポアソン比 | 0.35 |
| 密度 | 2700 kg/m3 |
| 粘性減衰係数 | 0.0002 |
(※この材料特性は、アルミニウムの物性値を基本としつつ、より変形がわかりやすくなるようヤング率を実際の1/20の値にしています。また粘性減衰係数は適当な値で設定しています。)
以下、この物体を「金属板」と呼ぶことにしましょう。
この金属板を次の条件に従って直線搬送します。
| 搬送時間 \(t_\mathrm{c}\) | 0.1 s |
|---|---|
| 搬送距離 \(s_\mathrm{c}\) | 0.2 m |
このとき金属板は、搬送時の慣性による力を受けることで、前後に反るように変形を起こすはずです。
したがって、ここでは、この金属板を直線搬送する際に、変形を最小限に抑えることが可能な「搬送パターン」を求めることが問題となります。
CAEモデルの作成
次に、コンピュータ上で金属板の搬送をシミュレーションするためのCAEモデルを作成します。
CAEモデルの基本的な作成手順は次のようになります。
(1) CADによる形状作成
(2) 形状のメッシュ分割
(3) 各種解析条件の設定
ここで(2)におけるメッシュは、要素を四面体とし、次のように分割をおこないました。

このときメッシュの要素数は7,038個となりました。
このモデルに対し動的変形解析をおこなうことで、搬送のシミュレーションを行なうことができます。
等速度での搬送
搬送パターンの最適化を行う前に、まずは基本的なパターンで金属板の搬送を解析してみましょう。
最初に、最もシンプルな搬送パターンであると考えられる、「等速度」での搬送をおこなってみます。
先に定義したとおり、搬送の条件としては、0.1 sの間に0.2 mの距離を搬送することでしたので、等速度での搬送は次のようなグラフとして表すことができます。
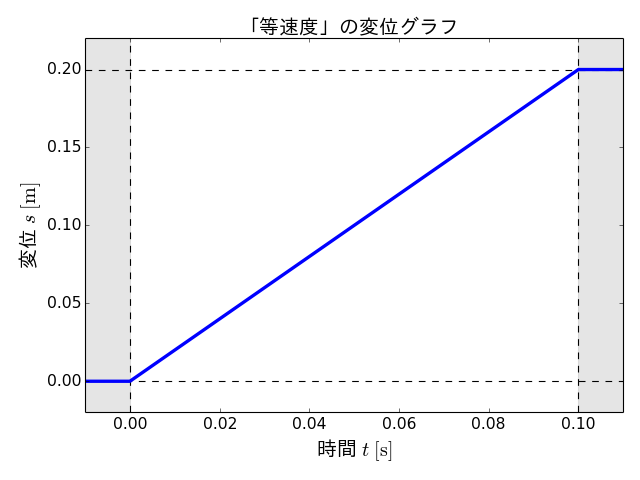
このグラフにおいて、横軸の\(t\)は搬送開始時刻からの経過時間を、縦軸の\(s\)は初期位置からの金属板の変位を表しています。
ここで、変位\(s\)は、時間\(t\)の関数として、
\begin{align*}
s = s(t)
\end{align*}
と表すことができます。この関数\(s(t)\)が、いわゆる「搬送パターン」の数学的・力学的な表現であるといえます。
それでは、この等速度での搬送パターンをCAEモデルに適用し、解析をおこなってみましょう。
解析結果は次のようになりました。
この動画からわかるとおり、金属板は大きく前後に振動しながら搬送されています。また、搬送の開始時および終了時にとくに大きな変形が発生していることがわかります。
この金属板の変形は、次のようなグラフとして表すことができます。
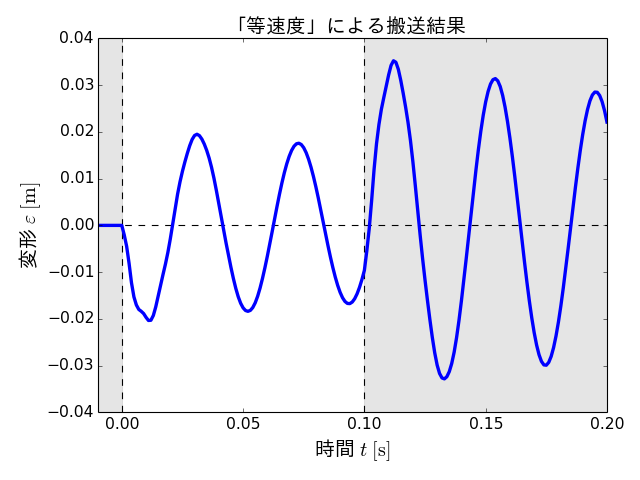
このグラフは、金属板土台に対する金属板最上部の相対位置を、金属板の変形\(\varepsilon\)として、時刻ごとにプロットしたものです。
このグラフより、搬送開始直後に不安定な振動が発生し、また搬送終了直後にも振動の振幅(すなわち変形)が大きくなっていることがわかります。
また、変形が最大となったのは、搬送終了後の時刻0.112 sのときで、そのときの変形量は0.0352 mでした。
以上の結果より、等速度による搬送は、かなり悪いものであるといえそうです。
ところで、この原因は何によるものなのでしょうか?
これを調べるために、等速度での搬送パターンを分析してみましょう。
まず、変位\(s(t)\)を時間\(t\)で微分してみます。すると次のような速度\(v(t)\)のグラフが得られます。
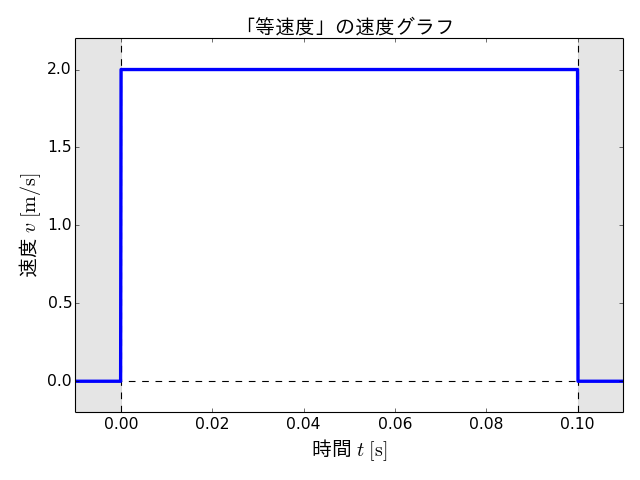
これは、0 sから0.1 sまでの区間が2.0 m/sで一定、すなわち、その名のとおりの等速のグラフとなっています。
この速度\(v(t)\)をさらに時間\(t\)で微分すると、加速度\(a(t)\)のグラフが得られます。
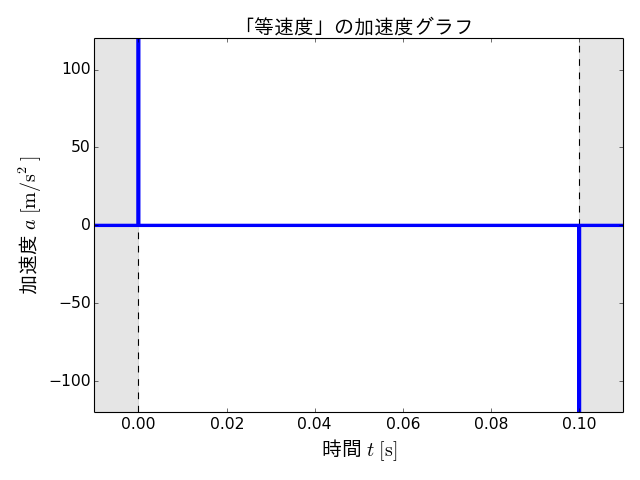
この加速度は、0 sと0.1 sの一瞬のみ、理論上それぞれ無限大とマイナス無限大をとり、それ以外の時刻では0となります。
ところで、力学的な観点からは、「運動の第2法則」より、加速度と力には比例の関係があります。
したがって、この等速度による搬送は、搬送開始の0 sと搬送終了の0.1 sにおいて、金属板には理論上、無限大の力がかかります。
つまり、この金属板の大きな変形は、このような無限大の力が原因であったといえます。
以上のことから、搬送の際の金属板の変形や振動の大きさは、搬送パターンの加速度の大きさが影響しているといえそうです。
変形正弦での搬送
続いて、等速度の他にもう一つ基本的な搬送パターンでの解析をおこなってみましょう。
使用する搬送パターンは「変形正弦」と呼ばれるものです。
変形正弦の変位、速度、加速度の各グラフは以下のようになります。
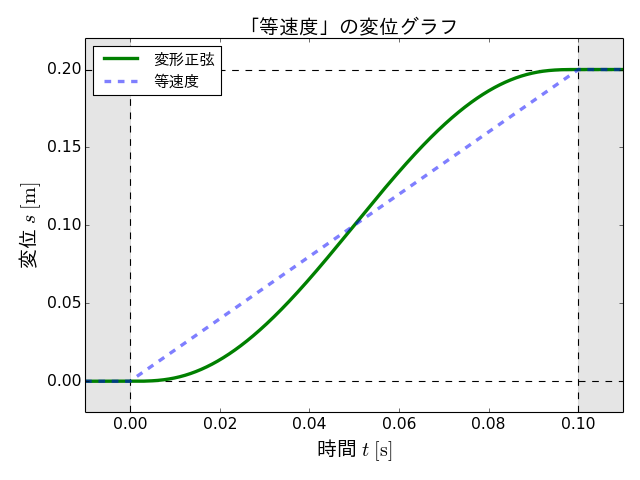
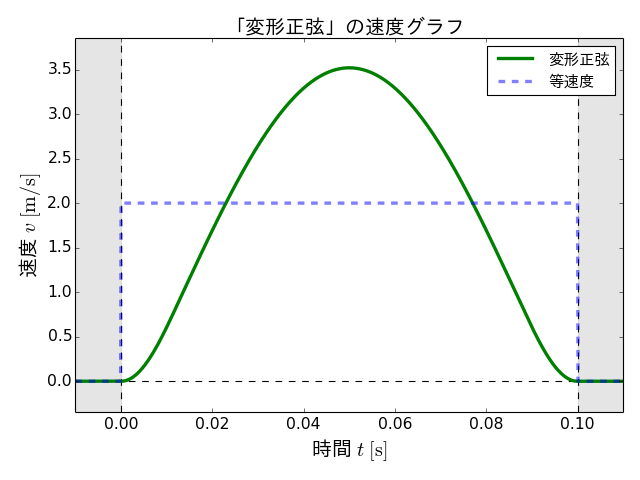
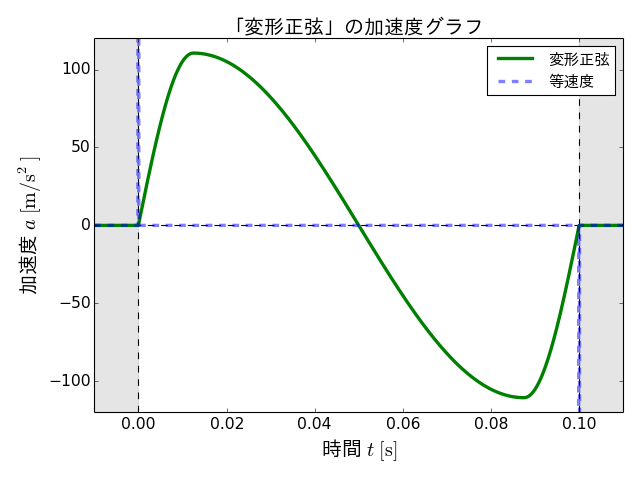
なお、これらの図には、等速度の各グラフも比較のために載せてあります。
問題の加速度は、等速度の場合と異なり、有限の値に収まっていることがわかります。
この変形正弦による搬送シミュレーションの結果は、次のようになりました。
また、このときの変形のグラフは次のようになります。
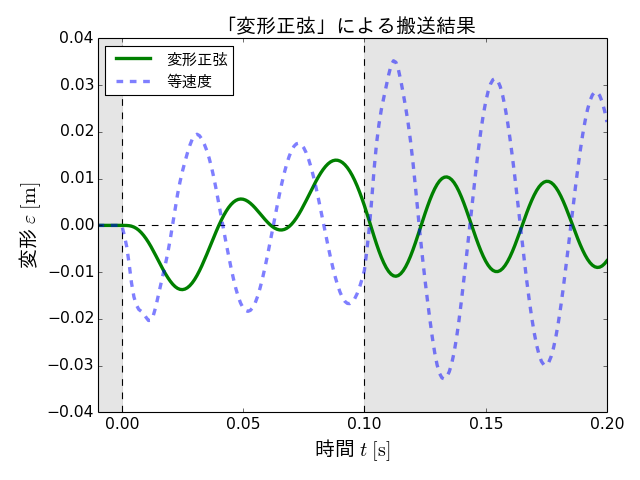
変形が最大となったのは、時刻0.088 sのときで、変形量は0.0139 mでした。
これは、等速度の場合の0.0352 mと比べ、半分以下と良好な結果となりました。
したがって、この直線搬送プロセスでは、等速度よりも変形正弦を用いたほうがより良い搬送が行えるでしょう。
本章では、与えられた設計問題をもとに、CAEモデルの構築をおこない、さらに等速度および変形正弦という搬送パターンにより、CAE解析をおこないました。
解析の結果、変形正弦は等速度よりも、金属板の変形をより低減させた搬送を実現可能なことがひとまずわかりました。
しかしながら、この変形正弦が、すべての搬送パターンのなかでベストであるとも限りません。せっかくなら、この変形正弦よりも優れた「最適な」搬送パターンを使用したいものです。
そこで次章からは、いよいよ最適化により、金属板の変形・振動をさらに抑制可能な搬送パターンを求めていきたいと思います。

